MENSURATION
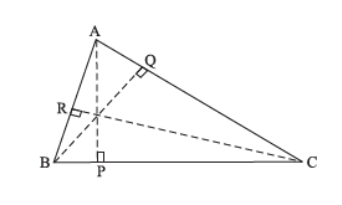
AREA OF A TRIANGLE 1. Area =1/2 × base × corresponding altitude
Area of Δ ABC =1/2× BC × AP
=1/2× AC × BQ
=1/2× AB × CR
2. Heron's formulaSemi-perimeter of Δ ABC’s =(a + b + c)/2Area of Δ ABC =
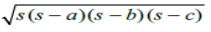
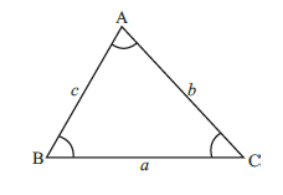
3. Area of Δ ABC = ½ × (Product of two sides) × (Sine of the included angle)
=1/2 ac sinB
=1/2ab sin C
= 1/2 bc sin A
4.Area of an Equilateral Triangle=(√3/4)(side)2

Note that
(i) among all the triangles that can be formed with a given perimeter, the equilateral triangle will have the maximum area.
(ii) For a given area of triangle, the perimeter of equilateral triangle is minimum.
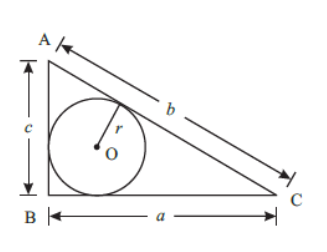
5.Area of Incircle and Circumcircle of a Triangle
(i) If a circle touches all the three sides of a triangle, then it is called incircle of the triangle.Area of incircle of a triangle = r. ss = (a + b + c)/2
For an equilateral triangle,

where h is the height of the triangle.
(ii) If a circle passes through the vertices of a triangle, then the circle is called circumcircle of the triangle.Area of the circumcircle = (abc)/4R
For an equilateral triangle,
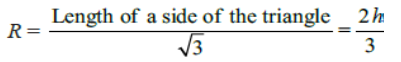
where h is the height or altitude of the equilateral triangle.Hence for an equilateral triangle, R = 2r.Note that an equilateral triangle inscribed in a circle will have the maximum area compared to other triangles inscribed in the same circle.
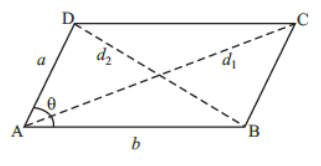
AREA OF A QUADRILATERAL
1. Area of quadrilateral ABCD=1/2 × (Length of the longest diagonal) × (Sum of length of perpendicular to the longest diagonal from its opposite vertices)
=1/2× d × (p1 + p2), where d = AC (i.e. longest diagonal)

2. If length of four sides and one of its diagonals of quadrilateral ABCD are given, then Area of the quadrilateral ABCD = Area of Δ ABC + Area of Δ ADC
3. Area of circumscribed quadrilateral
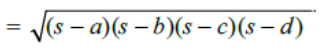
where s =(a + b + c + d)/2 and a, b, c, d are length of sides of quadrilateral ABCD.

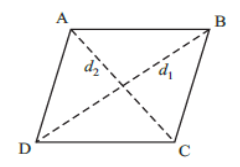
4. If θ1 and θ2 are the angles between the diagonals of a quadrilateral, then Area of the quadrilateral
=(1/2)d1 d2 sin θ1 or
=(1/2)d1 d2 sin θ2
Here d1 and d2 are the length of the diagonals of the quadrilateral.

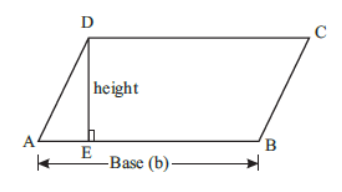
Area of a ParallelogramArea of parallelogram = Base × Corresponding height
A = b × h
Perimeter of a parallelogram = 2(a + b), where a and b are length of adjacent sides.
i.e., d12 + d2 2 = 2 (a2 + b2)
If θ be the angle between any two adjacent sides of a parallelogram whose length are a and b, then Area of parallelogram = ab sin θ
Note that in a parallelogram sum of squares of two diagonals
= 2 (sum of squares of two adjacent sides)
Area of a Rectangle

Area of a rectangle = Length × Breadth = l × b
Perimeter of a rectangle = 2(l + b)
Area of a Square
Area of square = side × side = a × a = a2
Length of diagonal (d) = a2 (by Pythagoras theorem)
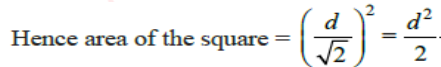
Perimeter of square = 4 × side = 4 × a
For a given perimeter of a rectangle, a square has maximum area.
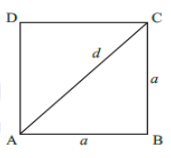
Note that the side of a square is the diameter of the inscribed circle and diagonal of the square is the diameter of the circumscribing circle.
Area of a Rhombus
Area of a rhombus =1/2 × product of diagonals
=1/2 × d1 × d2
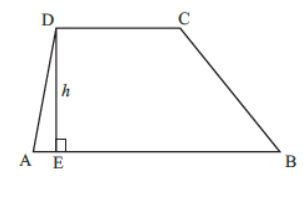
Area of a Trapezium
=1/2× (AB + CD) × DE
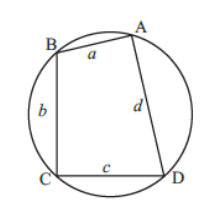
Area of a Cyclic Quadrilateral
For a given quadrilateral ABCD inscribed in a circle with sides measuring a, b, c, and d;
Area;-
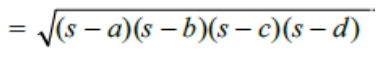
SURFACE AREA AND VOLUME OF SOLIDS
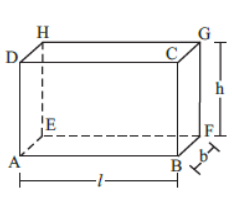
Cuboid
Total surface area of a cuboid = 2 (lb + bh + hl)
Lateral surface area (i.e., total area excluding area of the base and top) = 2h (l + b)
Length of a diagonal of a cuboid = l2 + b2 + h2
Volume of a cuboid = Space occupied by cuboid
= Area of base × height = (l × b) × h = lbh
Cube
A cube is a cuboid whose all edges are equal i.e.,
length = breadth = height = a (say)
Total surface area of the cuboid = Area of 6 square faces of the cube
= 6 × a2 = 6a2
Lateral surface area of cube i.e., total surface area excluding top and bottom faces = 4a2
Length of diagonal (d) of the cube
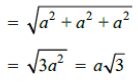
Volume of the cube (V) = Base area × Height
= a2 × a = a3
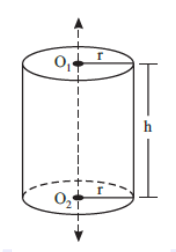
Cylinder
Curved surface area of a cylinder= Circumference of base × height
= 2πr × h = 2πrh
If cylinder is closed at both the ends then total surface area of the cylinder
= Curved surface area + Area of circular ends
= 2πrh + 2 × πr2 = 2πr(h + r)
Volume of the cylinder (V) = Base area × Height
= πr2 × h = πr2h
* Note that a cylinder can be generated by rotating a rectangle by fixing one of its sides.
Hollow Cylinder
Inner radius = ri and outer radius = ro,
Hence ro – ri = thickness of material of the cylinder.
Let length or height of the cylinder = h,
C.S.A = Outer curved surface area of the cylinder + Inner curved surface area of the cylinder
= 2π roh + 2πrih = 2πh(ro + ri)
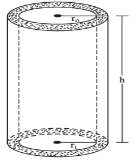
Total surface area of hollow cylinder
= C.S.A. of hollow cylinder + Area of 2 circular end rings.
= 2πh(ro + ri)+ 2π (ro2 – ri2)
= 2π (ro + ri) (h + ro + ri)
Volume of hollow cylinder = Volume of the material used in making the cylinder
= π (ro 2 – ri 2) h
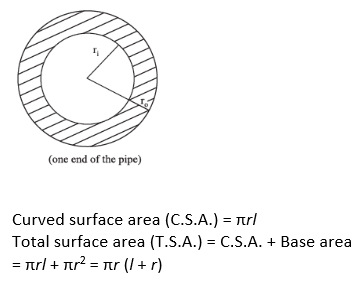
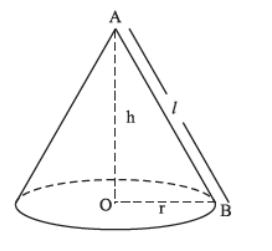
Cone
A cone is a solid obtained by rotating a strip in the shape of a right-angled triangle about its height. It has a circular base and a slanting lateral curved surface that converges at a point.
Its Slant height (l) = h2 + r2
Volume of cone =1/3× base area × height =1/3× r2 × h
When a conical cup of paper (hollow cylinder) is unrolled, it forms a sector of a circle Conical cup of paper Unrolled conical cup, which is a sector of a circle.Unrolled conical cup, which is a sector of a circle.
Radius of this sector is equal to slant height of the cone.Length of curved edge of this sector is equal to the circumference of the base of the cone.

Sphere
A sphere is formed by revolving a semi-circle about its diameter.
It has one curved surface which is such that all points on it are equidistant from a fixed point within it, called the centre.
Length of a line segment joining the centre to any point of the curved surface is called the radius (r) of the sphere.
Any line segment passing through the centre and joining two points on the curved surface is called the diameter (d) of the sphere.
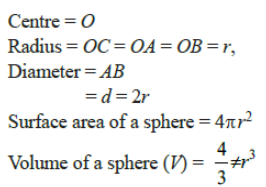
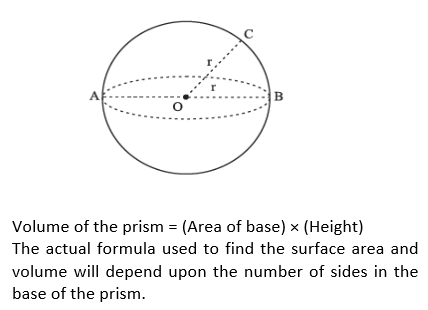
Prism
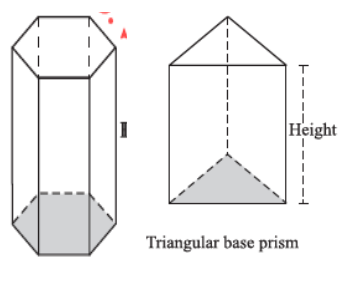
A ‘prism’ is a solid having identical and parallel top and bottom (or base) faces. These identical faces are regular polygon of any number of sides. The side faces of a prism are rectangular and are known as lateral faces. Number of lateral faces is equal to the number of sides in the base. Here are some examples of prisms Lateral surface area of the prism = (Perimeter of the base) × (Height)
Total surface area of the prism = (Surface area of the top and bottom) + (Lateral surface area)= 2 × Area of the base + Perimeter of base × Height
Pyramid
It is a three-dimensional body made up of a regular polygon shaped base and triangular lateral faces that meet at a point called vertex, which is also called the apex of the pyramid.
The number of triangular faces is equal to the number of sides in the base.
For example: A pyramid with a square base has four triangular faces, whereas a pyramid with a hexagonal face is made up of six triangular faces, and so on.
Lower face is called the base and the perpendicular distance of the vertex (or top) from the base is called the height or altitude of the pyramid.
The altitude of a lateral face of a pyramid is the slant height, which is the perpendicular distance of the vertex (or top) from the mid-point of any side of the base.
The lateral surface area of a regular pyramid is the sum of the areas of its lateral faces.
Lateral surface area of a pyramid=1/2× (Area of the base) × (Slant height)
Total surface area of a pyramid=1/2× (Perimeter of the base)× (Slant height) + (Area of the base)
Volume of a pyramid =1/3× Area of base × Height

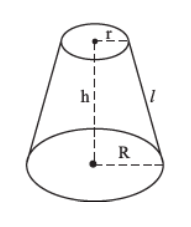
Frustum of a Cone
When top portion of a cone cut off by a plane parallel to the base of it, the left-over part is called the frustum of the cone.

EULER'S RULE
For any regular shape solid (like cuboid, cube, cylinder, etc)
Number of faces (F) + Number of vertices (V)
= Number of edges (E) + 2
i.e., F + V = E + 2
EXERCISE
Q.1:What is the perimeter (in cm) of an equilateral triangle whose height is 3.46 cm ?Take \sqrt 3= 1.73.
(A) 12
(B) 9
(C) 6
(D) 10.4
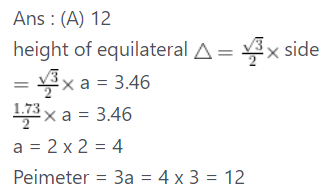
Q.2:The perimeters of two similar triangles ABC and PQR are 156 cm and 46.8 cm respectively. If BC = 19.5 cm and QR = x cm, then the value of x is:
(A) 3.76 cm
(B) 5.85 cm
(C) 4.29 cm
(D) 6.75 cm

Q.3:The radius of a sphere is 9 cm. It is melted and drawn into a wire of radius 0.3 cm. The length of the wire is:
(A) 112 m
(B) 108 m
(C) 118 m
(D) 106 m

Q.4: One side of a rectangular field is 39 m and its diagonal is 89 m. What is the area of the field ?
(A) 3120 m2
(B) 2100 m2
(C) 2160 m2
(D) 3140 m2

Q.5: The base of a triangle to the perimeter fo a square whose diagonal is 7\sqrt2 cm and its height is equal to the side of square whose area is 169 cm2 . The area (in cm2 ) of the triangle is:
(A) 130
(B) 182
(C) 175
(D) 156
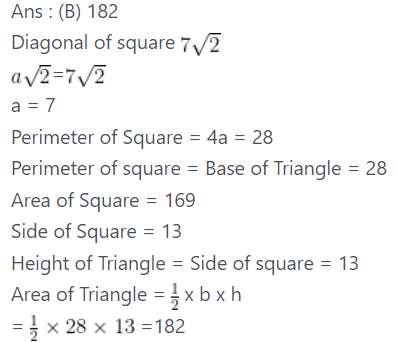
Q.6: If the adjacent sides of a rectangle whose perimeter is 60 cm are in the ratio 3 : 2, then what will be the area of the rectangle ?
(A) 864 cm2
(B) 216 cm2
(C) 60 cm2
(D) 300 cm2

Q.7: The perimeter of a right angle triangle whose sides that make right angles are 15 cm and 20 cm is:
(A) 60 cm
(B) 40 cm
(C) 70 cm
(D) 50 cm
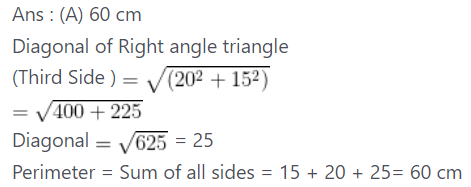
Q.8: The difference between the two perpendicular sides of a right-angled triangle is 17 cm and its area is 84 cm2 . What is the perimeter (in cm ) of the triangle ?
(A) 65
(B) 49
(C) 72
(D) 56
